Mechanical Vibration System with Dynamic Displacement of Long Suspension Bridge

Abstract

Abstract: This work presents an algorithm that automatically identifies the equivalent mass and speed of vehicles crossing a long-span suspension bridge utilizing ambient vibrations data. The first goal is to estimate vehicle characteristics that can be further used to gather information about the level of serviceability loading of the bridge, as well as provide relevant data for smart asset management. Sensors are used to measure the vibrations and secondary inputs to the system are used to actuate the flexible body in order to obtain some desired structural response. As that, for longer span bridges the change in stiffness of the track has a negligible effect on the acceleration and displacement. All analysis have done using MATLAB tool.

Introduction

I. INTRODUCTION

Vibrations are oscillations in mechanical dynamic systems. Although any device can oscillate while  it  is  compelled  to  do  so  externally,  the  term  “vibration”  in  mechanical  engineering  is  regularly reserved for structures that could oscillate freely without carried out forces. Sometimes those vibrations reason  minor  or  severe performance  or  protection  troubles  in  engineered  systems.   For  instance, whilst  an  plane  wing  vibrates  excessively,  passengers  in  the  aircraft  come to be uncomfortable in particular whilst the frequencies of vibration correspond to herbal frequencies of the human frame and  organs.   In  fact,  it  is  nicely  recognized  that  the resonant  frequency  of  the  human  intestinal  tract (approx.  Four-eight  Hz)  should  be averted at  all  charges  while  designing  excessive  overall performance  aircraft  and reusable  release  motors  due to the fact  sustained  exposure  can  cause  severe  inner  trauma.

If  an  aircraft  wing  vibrates  at  massive amplitudes for an prolonged time period, the wing will sooner or later enjoy a fatigue failure of some  kind,  which  might doubtlessly  motive  the  aircraft  to  crash  resulting  in  injuries  and/or fatalities.   Wing  vibrations  of  this  kind  are  usually  related  with  the  huge  variety  of flutter phenomena added on through fluid-shape interactions.

Magnetostrictive materials generate strength from the huge variant in magnetic fields that rise up as a result of wind prompted vibration. Magnetostrictive substances along with Fe–Ga alloy [1], validated excessive sensitivity to the implemented pressure and have a simple structure as proven in Fig 1.1. In  analyzing  books  and  technical  papers  on  vibration  together with  the  previous  paragraph, engineering  college students  are  commonly  left  with  the  influence  that  all vibrations  are  negative because  maximum  publicized  paintings  discusses  vibration discount  in  one  shape  or  another.  But vibrations can also be useful. For instance, many distinctive sorts of mining operations rely upon sifting vibrations via which distinct sized particles are looked after the usage of vibrations. In nature, vibrations are also utilized by all types of one-of-a-kind species of their everyday lives.

Orb web spiders, for instance,  use  vibrations  in  their  webs  to  discover  the  presence  of  flies  and  other bugs  as  they conflict after being captured inside the net for meals. The motive that mechanical structures vibrate freely is because energy is exchanged between the system’s inertial (masses) elements and elastic (springs) factors. Free vibrations commonly stop after a certain length of time because damping factors in systems use up strength as it's far transformed lower back-and-forth among kinetic strength and potential energy.

The function of mechanical vibration evaluation should be to use mathematical equipment for modeling and predicting capacity  vibration  issues  and  solutions,  which  are  normally  now not  obvious  in preliminary engineering designs. If issues may be anticipated, then designs can be changed to mitigate  vibration  problems earlier than  systems  are  manufactured.   Vibrations  can  additionally  be deliberately delivered into designs to take advantage of advantages of relative mechanical movement and to resonate structures (e.g., scanning microscopy). Unfortunately, expertise of vibrations in initial  mechanical  designs  is  not often  considered  critical,  so  many  vibration  research  are carried  out  only  after  systems  are  synthetic.   In  those  cases,  vibration  problems  must  be addressed using passive or lively layout changes. Sometimes a layout change can be as easy as a thickness change in a vibrating panel; brought thickness tends to push the resonant frequencies of a panel higher main to less vibration inside the operating frequency variety. Design changes also can be as complicated as placing magneto-rheological (MR) fluid dampers into mechanical systems to take energy faraway from vibrating systems at precise times at some point of their motion.

This work is introduced as pursues. In Section II, It portrays the introduction of bridge model with their parameter identification. Section III provides description of proposed system. Section IV describes the main results of system. At last, conclusion is clarified in Section V.

II. BRIDGE MODEL

An accurate Finite Element (FE) model of structures plays a very important role in many applications in the field of civil engineering, such as health monitoring, non-destructive damage detection, structural assessment and control, etc. In the study of bridge-vehicle coupled vibration, the bridge model is also one of the three major factors (the other two being the vehicle model and road roughness) that determine the responses of both the bridge and vehicle. However, a newly-created FE bridge model is usually not accurate and may or may not truly represent the physical characteristics of the real structure due to modelling errors, and simplifications and/or assumptions made in the modelling process.

A number of model updating methods have been proposed in the literature. A comprehensive review of the FE model updating techniques and their applications to damage detection. In some works non-iterative methods were used, which directly updates the elements of stiffness and mass matrices in one-step. Using this method, the updated stiffness and mass matrices can reproduce the measured modal responses exactly. However, structural connectivity is usually lost in the updating process. As a result, the updated mass and stiffness matrices are not always physically meaningful. In other works, iterative parameter-updating methods were employed. These methods use the sensitivity matrix of the parameters, which can be obtained by conducting sensitivity studies with respect to the parameters, in the model updating process. These sensitivity-based parameter-updating methods have an advantage of modifying parameters that can directly affect the dynamic characteristics of the structure, and as a result, explanations for the updated parameters are available. Most of these model updating methods in the literature have demonstrated their abilities to achieve agreements between the measured bridge responses and the predicted bridge responses from the updated model to some extent. However, accurate mode shape and modal curvature cannot be easily obtained from field testing, while natural frequencies alone are not enough to update a FE model of a bridge successfully.

A. Identification of Dynamic Vehicle Loads

Bridges in service are subject to a combination of various external loads, among which a very important load is the traffic load. The dynamic vehicle load information is very important for designing new bridges, assessing the condition of existing bridges, and maintaining old bridges. Vibration of bridges is induced mainly due to the road roughness and dynamic traffic loads. Under certain circumstances, the dynamic effect of bridges can be significant. However, most current weigh-in-motion techniques usually require a smooth road surface or slow vehicle movement in order to reduce the vibration of the bridge and dynamic effect of vehicles. As a result, they usually measure only the static axle loads.

In an early model developed by O’Conner and Chan (1988), the bridge was modelled as an assembly of lumped masses interconnected by massless elastic beam elements. This model has usually been referred to as the Beam-Element Model. Continuous Beam Models with constant cross-section and constant mass per unit length were developed later by other researchers, either in the form of a simply supported beam or a multi-span continuous beam.

B.  Parameter Identification of Vehicles

Another research branch generated from the research of bridge-vehicle interacted vibration is parameter identification of vehicles (usually referred to as a system identification problem), which essentially belongs to an optimization problem. Research has found that vehicle properties (such as stiffness and damping) have a great impact on the bridge-vehicle interacted vibration. In highway engineering, vehicles that cause more damage than others are usually referred to as road-unfriendly vehicles. Similar to the identification of moving loads on bridges, parameter identification of vehicles is also an inverse problem, with the forward problem aiming to obtain the bridge responses given that the vehicle properties are known. Belonging to an optimization problem, this problem is, however, different from the problem of identifying moving loads in the sense that the moving loads can be calculated directly from the equation of motion for the bridge vehicle coupled system while the vehicle parameters cannot be obtained in a similar way.

For the bridge model, the modified beam functions proposed. It presented a parameter identification method based on the dynamic response sensitivity analysis. The modified beam were also used for the bridge, and a twelve-parameter vehicle model was used for the vehicle. The identification was realized based on the least-squares method with regularization from the measured strain, velocity, or acceleration.

In most previous works the bridge was modelled as a simple beam (or one dimensional beam). As a result, the vehicle model was usually limited to a SDOF system or two-DOF system. All the beam-model-based methodologies would become impractical if the entire structure of a complicated bridge is to be modelled for applications. Moreover, the oversimplified vehicle models may not be able to well represent the real vehicles travelling on bridges. In the present study, the GA was used to identify the parameters of more realistic vehicle models. A series of case studies are carried out in which the effects of various factors such as measurement station, vehicle speed, travelling route, number of vehicles, road surface condition, and noise level are numerically investigated. Bridge responses, including displacement, strain, and acceleration, were all used in the identification process. The developed methodology was also applied to identify the parameters of a real truck travelling through a field bridge using the measured bridge responses. Results show that the developed methodology can be used to identify the static weight of vehicles travelling though bridges with satisfactory accuracy.

III. DESCRIPTION OF VIBRATION BASED BRIDGE SYSTEM

To describe the dynamic vibrations of the deck, the bridge is modelled using a continuum model to reduce the computational cost associated with the identification of the vehicles. The initial motivation to instrument the Lysefjord Bridge with a WASHMS was to study its buffeting response, including the torsional response of the bridge around its longitudinal axis. For this reason, pairs of accelerometers were installed inside the girder. Since the bridge main span has a width of 12.3 m for a length of 446 m, it was modelled as a line-like structure. The records from each pair of accelerometers were thus combined to compute the lateral, vertical, and torsional bridge acceleration response, at the four measurement locations.

In the present study a single degree-of-freedom (SDOF) system consisting of a mass, spring, and damper was used to establish the vehicle-bridge coupling equations and to demonstrate how the proposed method works out. The SDOF system has proved adequate to simulate the interaction between a single wheel (or vehicle) and the bridge deck. It should be noted that the methodology can similarly be applied to a full scale multi-degrees-of-freedom (MDOF) vehicle model, which is usually represented by a combination of rigid bodies connected by a series of springs and damping devices. The equation of motion of a vehicle can be written as below according to Newton’s Second Law by (1):

where M is the mass of the vehicle; a is the acceleration of the vehicle in the vertical direction; F is the gravity force of the vehicle; and Fv is the interaction force between the vehicle and bridge deck.

A. Speed Profile Module

The speed profile module allows to define two kind of speed profiles: a predefined speed profile and an arbitrary speed profile. Note that all the speed profiles are expressed in the angle domain. The predefined speed profile menu enables you to set the following parameters:

1. The sampling frequency of the desired simulated signal in Hz;
2. The number of points per revolution;
3. The frequency deviation

B.  Background Noise Module

In this module it is possible to add stationary Gaussian background noise by defining its mean and variance. Furthermore, it is possible to convolve the background noise with a given Impulse Response Function modelled as a Single-Degree-of-Freedom system which can be useful for testing blind separation and blind de-convolution techniques.

C. Signal Generation Module

Once set all the parameters, the signal can be generated and then saved through this module. The signal is saved as .mat file and the following variables will be provided:

1. A Vector variable that contains the simulated signal, called simulated Signal
2. A Vector variable that contains the response of the gear contributions only neglecting the background noise.

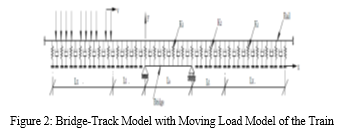
D. Bridge-Track Model

Track structure is added before and after the bridge in order to include the dynamic effect from the track structure over the bridge as shown in Fig 2.

The road surface condition is an important factor that affects the dynamic responses of both the bridge and vehicles. A road surface profile is usually assumed to be a zero-mean stationary Gaussian random process and can be generated through an inverse Fourier transformation based on a power spectral density (PSD) function.

Vehicles travelling on a bridge are connected to the bridge via contact points. The wheel road interaction forces acting on the bridge and the interaction forces acting on the vehicles are actually action and reaction forces existing at the contact points. In terms of finite element modelling, these interaction forces may not apply right at any element node. Therefore, the interaction forces need to be transformed into equivalent nodal forces Fb in the finite element analysis. According to the virtual work principle and the concept of shape function it is easy to understand that the work done by the actual force directly acting on one element F and by the equivalent nodal forces Fe should be equal.

For two interaction forces acting upon different positions of the same bridge, the corresponding Nb for the two forces would be different though the element shape function Ne may be the same, because the non-zero terms in the two force vectors are interaction force location dependent. When a vehicle travels on the bridge, the position of the contact point changes with time, which means the road roughness r(x) at the contact point and the shape function Nb are both time-dependent terms, indicating that all the additional terms are time-dependent terms.

While inertia forces are always included in dynamic simulations, their effect on the identified interaction forces was investigated since this effect was usually ignored in the bridge weigh-in-motion practice. The portion of bridge response caused by the bridge inertia force at each time point can be obtained using the following steps: First, the acceleration for each element (or node) on the bridge model can be obtained directly after running the numerical program; then, the inertia force of each element (or node) on the bridge model can be calculated as a product of the mass and acceleration of the element (or node). The effect of the inertia force of each element (or node) on the bridge response can then be obtained using influence surface concept; and finally, the effects of all elements (or nodes) on the bridge can be added to obtain the total effect of the total bridge inertia force on the response.

1. Input Variables

Input variables are provided in the MATLAB, which remain constant for one type of the bridge. These input variables include damping ratio, sleeper spacing, stiffness of ballast, stiffness of bridge and rail structure, span length and element size etc.

2. Create Bridge Structure

Bridge structure is created from these inputs during the analysis.

3. Create Loads and Amplitude

Moving load function (by john Leander) is used to create loads and amplitudes. These loads and amplitudes create moving load model of the train.

IV. RESULTS & DISCUSSION

The study of vehicle–bridge dynamic interaction is generally conducted by describing each vehicle as a multiple degree of-freedom system. In that case, the accurate modelling of the high-frequency bridge response is crucial to provide realistic results. The situation described here is fundamentally different as vehicles are detected using the quasi-static vertical bridge response only, that is, the frequency range located below the first eigen frequency. Besides, we focus only on the vertical displacement response of the Lysefjord Bridge, which is dominated by only few modes at frequencies below 1 Hz. Since the vehicle response is not studied here, a moving mass model53 is found adequate to investigate the vehicle-induced bridge response. The use of a moving mass model is also supported by the fact that the high-frequency range of the bridge displacement response is negligible compared to its low-frequency response. There is no specific single value for the track stiffness in the literature. Every author uses a different number for the track stiffness depending upon their model.

Analysis is made with different time steps by using moving load model of the train at Train. We can see from the graph that there is not that much difference in the results even for larger time step. To be more precise in the results a time step of 200 is selected for the analysis. The vertical acceleration response at midspan is transformed into the displacement response to amplify the influence of the low-frequency bridge response on its total motion. Figure 3 shows the results for vertical displacement of the bridge, when running moving load model of the train.

For each segment, the normalized bridge response can, therefore, be characterized in terms of vehicle arrival time and vehicle speed. The arrival time is defined here as the time at which the bridge response due to traffic loading is detected by the accelerometers at midspan and corresponds to the time at which a vehicle arrives on either the north side or the south side of the bridge's main span. For each cluster, these two parameters are simultaneously estimated by minimizing the RMSE value between the computed and recorded vertical response of the bridge deck at midspan.

Conclusion

This work presents an algorithm that automatically identifies the equivalent mass and speed of vehicles crossing a long-span suspension bridge utilizing ambient vibrations data. The first goal is to estimate vehicle characteristics that can be further used to gather information about the level of serviceability loading of the bridge, as well as provide relevant data for smart asset management. The second goal is to identify situations where the vehicle-induced response of the bridge can be exploited to estimate the bridge damping ratios using high-quality free-decay response. The identification of the vehicles relies on the analysis of the background component of the vertical displacement response..

References

[1] O. Oyuna, A. Angatkina, Y. Krauinsch, (2014), \" Interaction Features between the Drive System and the Oscillation System in the Hydraulic Volumetric Vibration Machine\", International Conference on Mechanical Engineering, Automation and Control Systems, pp. 01-05. [2] M. Griscenko, R. Helmanis, (2014), \"Power Generator Mechanical Faults Effects on Electric Power Quality\", IEEE, pp. 143-146. [3] K. Tao, S.W. Liu,J.M. Miao, (2014), \" A Three-Dimensional Electrostatic/Electret Micro Power Generator for Low Acceleration and Low Frequency Vibration Energy Harvesting\", IEEE MEMS, pp. 366-369. [4] X. Yang, Y. Wang, Y. Cao, (2014), \" A New Hybrid Piezoelectric-Electromagnetic Vibration-Powered Generator and Its Model and Experiment Research\", IEEE Transactions on Applied Superconductivity, Vol 24, No. 3, pp. 01-04. [5] Z. Wang, T. Yao, Z. Wang, (2015), \" The Analysis of Nonlinear System Characteristics of Vibration-To Electric Generator\", IEEE Transactions on Magnetics, pp. 01-04. [6] I. Thalji, E. Jantunen, (2015), \" A Summary of Fault Modelling and Predictive Health Monitoring of Rolling Element Bearings\", Mechanical Systems and Signal Processing, pp. 01-21. [7] W. Smith, R. Randall, (2015), \" Rolling Element Bearing Diagnostics Using The Case Western Reserve University Data: A Benchmark Study\", Mechanical Systems and Signal Processing, pp. 01-32. [8] D. Abboud, S. Baudin, J. Antoni, (2016), \" The Spectral Analysis Of Cyclo-Non-Stationary Signals\", Mechanical Systems and Signal Processing, pp. 01-21. [9] K. Ishida, J. Muranishi, T. Aoki, (2016), \"The Generation Characteristics of the Improved Configuration of the Stator and the Mover in the Linear Generator Using Vibration Energy \", IEEE, pp. 2634-2637. [10] M. Minami, T. Sakabe, (2018), \"An Experimental Verification for Improvement of Output Characteristics by LC Resonance in Vibration Generators with Boost Type Current Improving Passive Rectifier\", International Conference on Renewable Energy Research & Applications, pp. 164-167. [11] K. Hasegawa, T. Ueno, (2019), \" Proposal of Wind Vibrational Power Generator Using Magnetostrictive Material\", IEEE Transactions on Magnetics, pp. 01-04. [12] M. Buzzonia, G. D’Elia, (2020), \"A tool for validating and benchmarking signal processing techniques applied to machine diagnosis\", Mechanical Systems and Signal Processing, pp. 01-24. [13] K. Htoo, Z. Aung, (2020), \" Investigation of the Operation of a Single-Phase Synchronous Vibration Micro Generator and an Uninterrupted Power Supply Source for Autonomous Objects \", IEEE, pp. 979-982. [14] J. Zhang, H. Xu, X. Wang, (2021), \" Mechanical Defect Field Detection for Operational GIS Equipment Based on Vibration Signal Analysis\", IEEE Explore, pp. 1244-1248.

Copyright

Copyright © 2022 Manpreet Singh, Er. Ashok Kumar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.